238. Product of Array Except Self
June 2024
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i]. You must write an algorithm that runs in O(n) time and without using the division operation. The output array does not count as extra space for space complexity analysis.
Example
Input: nums = [1, 2, 3, 4]
Output: [24, 12, 8, 6]
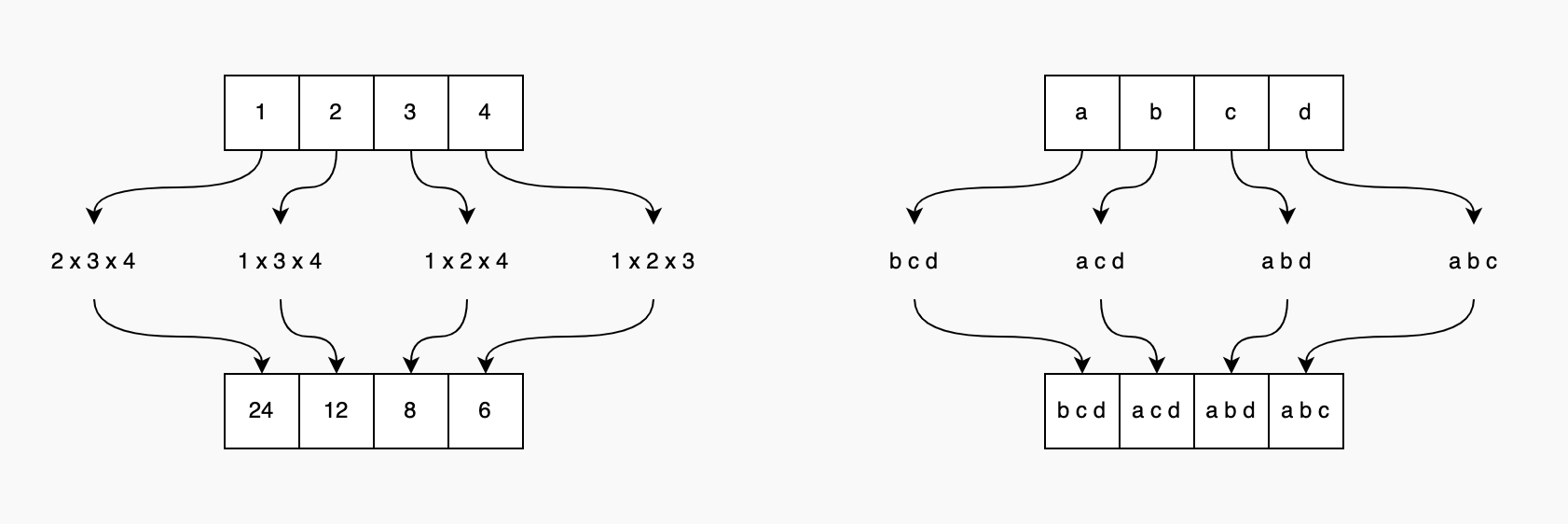
Brute Force Approach
Use nested for loops.
- The first (outer) loop iterates through the
numsarray - The second (inner) loop iterates over
numsarray again and calculates the product of all elements except the current element (index) from the first loop
1var productExceptSelf = function (nums) { 2 const res = new Array(nums.length) 3 4 for (let i = 0; i < nums.length; i++) { 5 let product = 1 6 for (let j = 0; j < nums.length; j++) { 7 if (i !== j) { 8 product = product * nums[j] 9 } 10 res[i] = product 11 } 12 } 13 14 return res 15}; 16
Time Complexity: O(n^2)
Space Complexity: O(1)
Since the question specifically says the algorithm should run on O(n) time, this is not a valid solution.
Optimized Approach 1
Calculate the product of all the elements in the array and divide this product by each element.
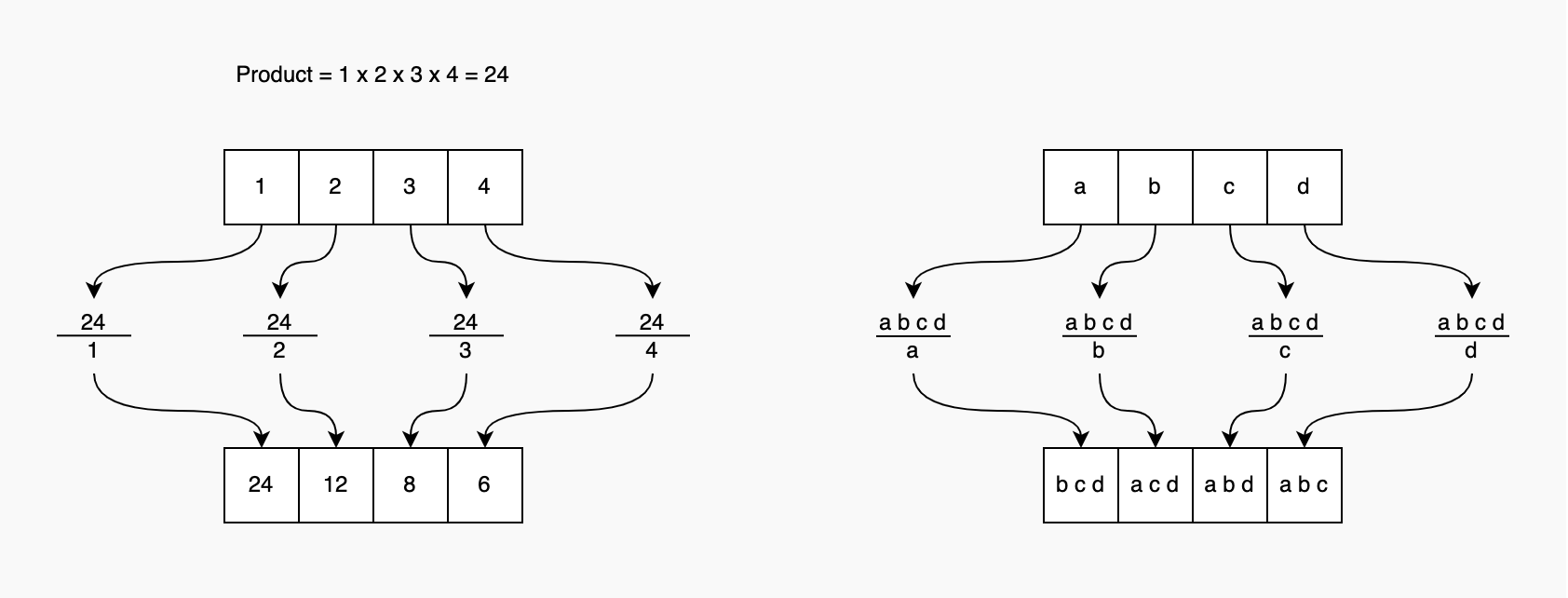
- Loop through and calculate the product of all the elements in
numsarray - Loop through
numsarray again and divide the product from the previous step by the current element - If there is exactly one zero in the
numsarray, the output for the position of that zero will be the product of all non-zero elements in the array. For all other positions, the output will be zero since their products will involve the zero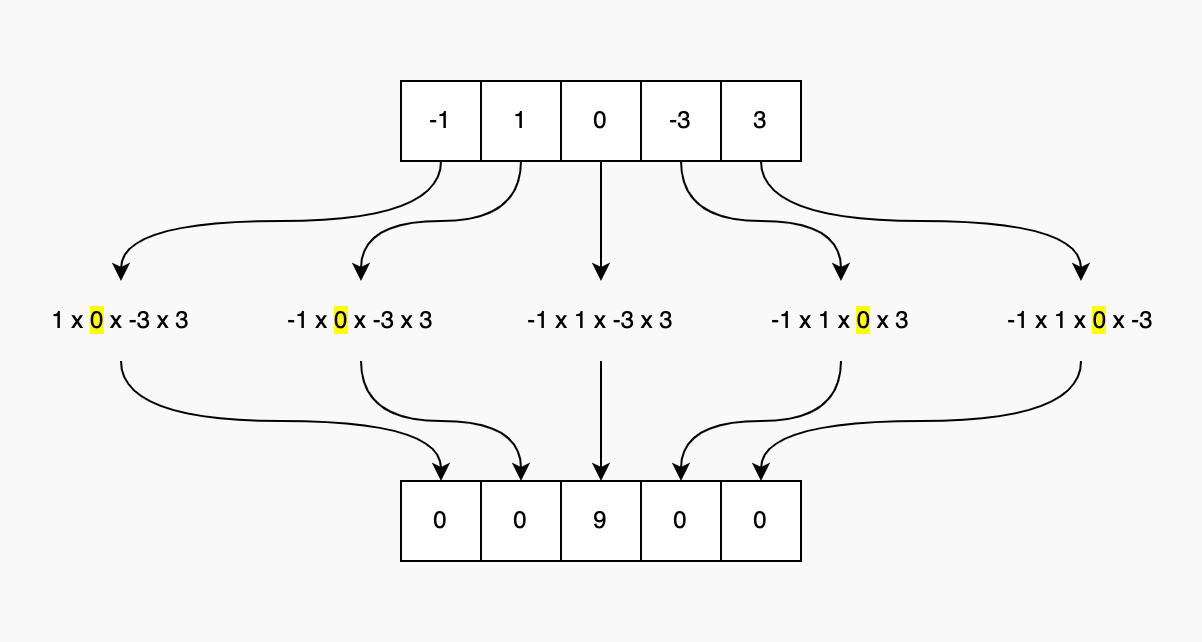
- If there are two or more zeros in the
numsarray, the output will always be zero for every element because any combinations of products will include at least one zero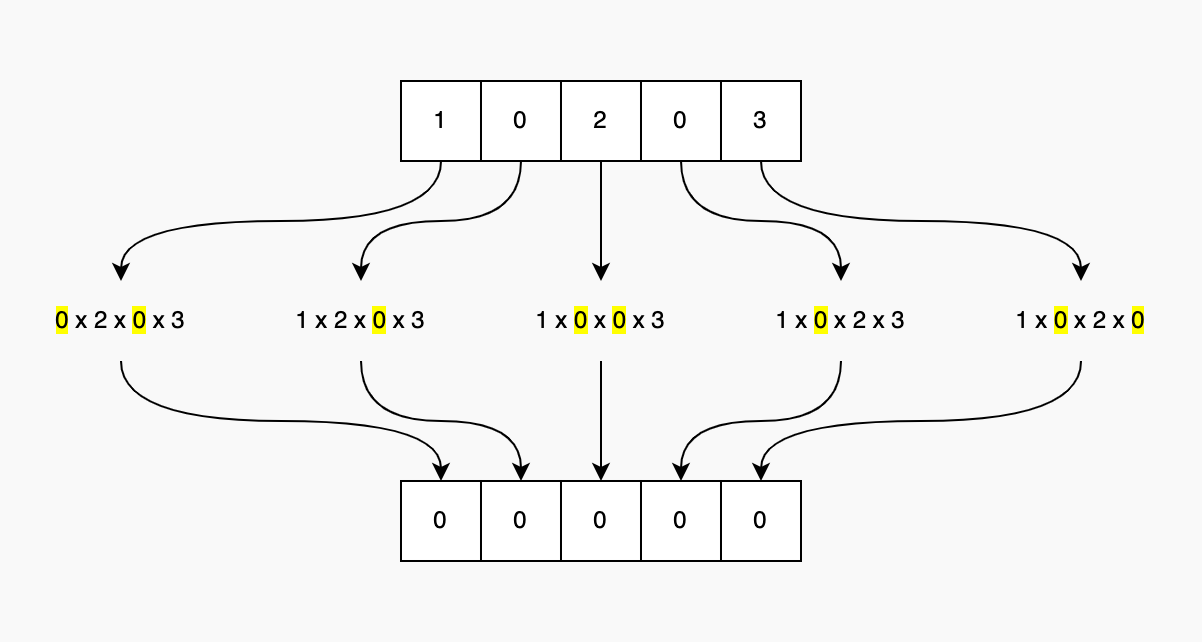
1var productExceptSelf = function (nums) { 2 const res = new Array(nums.length) 3 4 let product = 1 5 let zeroCount = 0 6 7 /* Calculate the product of all the elements and keep a track of number of zeroes */ 8 for (let i = 0; i < nums.length; i++) { 9 if (nums[i] === 0) { 10 zeroCount++ 11 } else { 12 product = product * nums[i] 13 } 14 } 15 16 // If there are two or more zeros in the array, 17 // the output will always be zero for every element 18 if (zeroCount > 1) { 19 return res.fill(0) 20 } 21 22 for (let i = 0; i < nums.length; i++) { 23 // If there is exactly one zero in the array, 24 // the output for the position of that zero 25 // will be the product of all non-zero elements in the array. 26 // For all other positions, 27 // the output will be zero since their products will involve the zero. 28 if (zeroCount === 1) { 29 if (nums[i] === 0) { 30 res[i] = product 31 } else { 32 res[i] = 0 33 } 34 } else { 35 res[i] = product / nums[i] 36 } 37 } 38 39 return res 40}; 41
Time Complexity: O(n)
Space Complexity: O(1)
Since the question specifically says the algorithm should not use the division operation, this is not a valid solution.
Optimized Approach 2
Use prefix and suffix products. Calculate the product of elements from the beginning of the array up to the element before the current one. Calculate another product of elements starting from the element next to the current one and till the end of the array. Multiplying the two products will give us the desired output.
- Prefix product is the product of all elements up to and including the current element for each position in the array
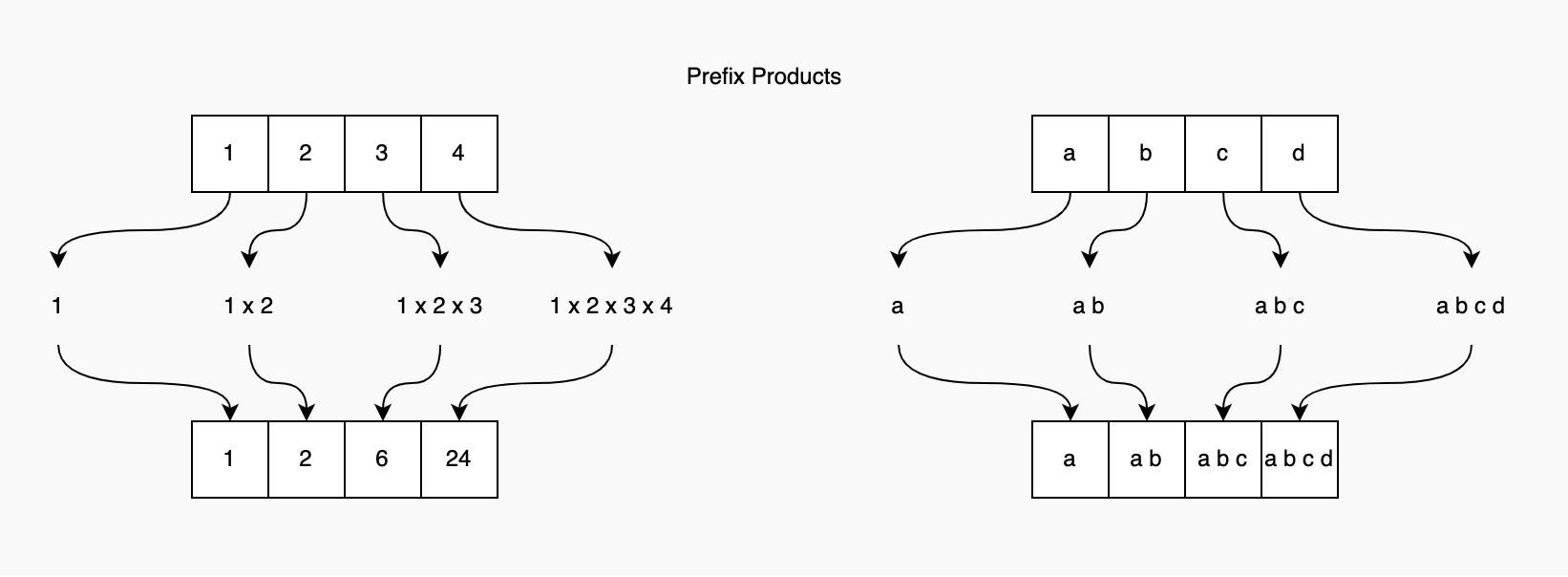
- Suffix product is the product of all elements after and including the current element for each position in the array
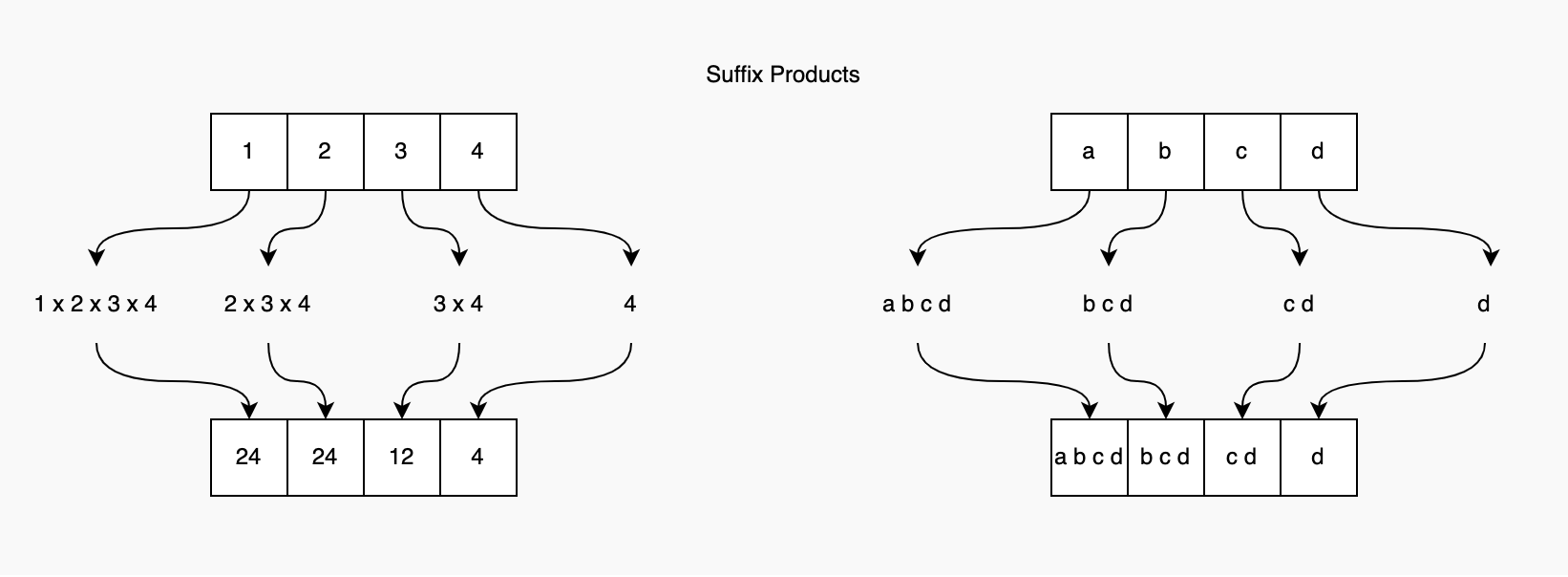
- The desired output at index
ican be calcuated byprefix[i-1] * suffix[i+1]- When
i = 0, sinceprefix[i-1]will not be available, the desired output issuffix[i+1] - When
i = n-1, sincesuffix[i+1]will not be available, the desired output isprefix[i-1] - For all other indexes, the desired output is
prefix[i-1] * suffix[i+1]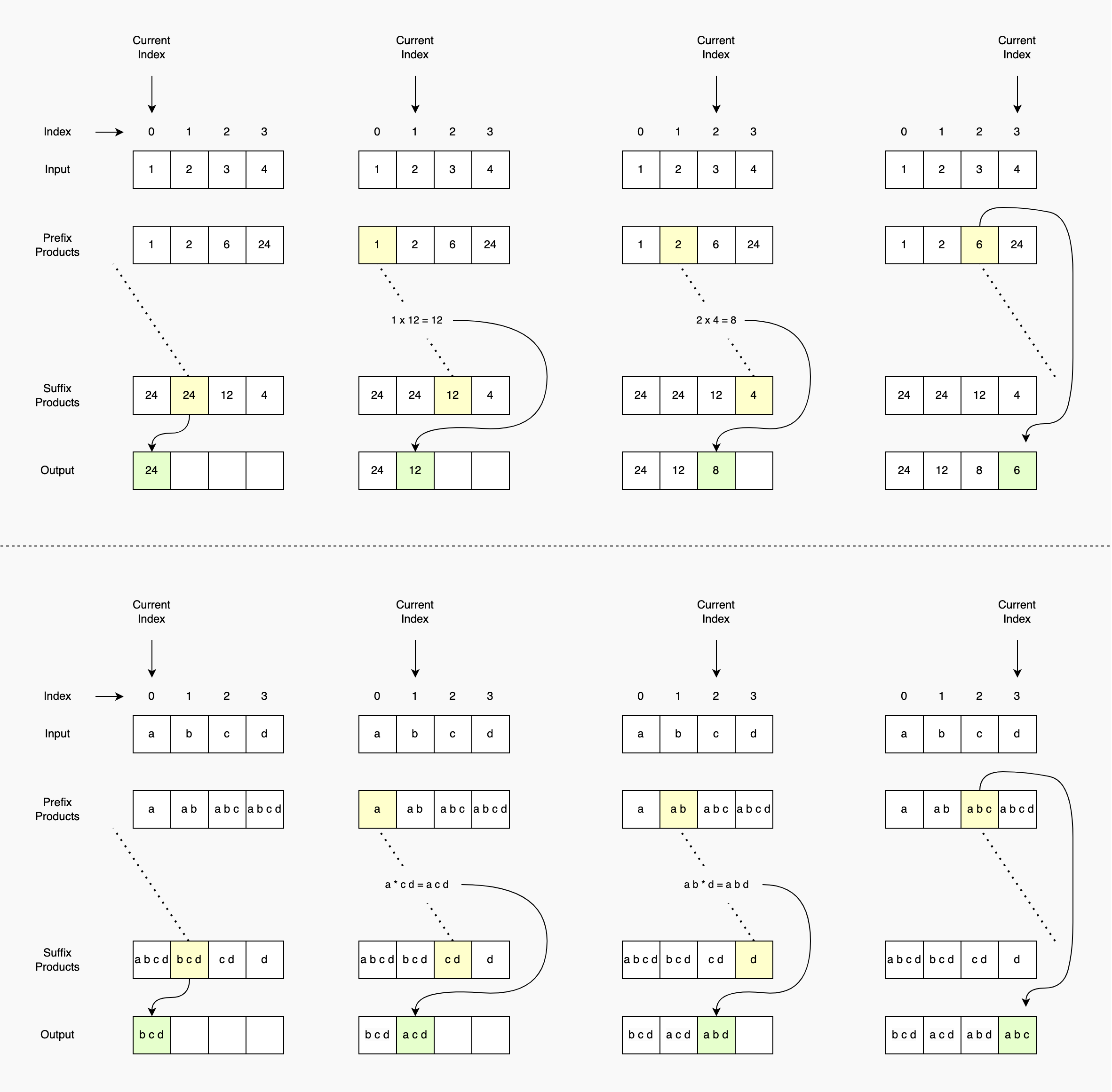
- When
1var productExceptSelf = function (nums) { 2 const prefixArr = new Array(nums.length) 3 const suffixArr = new Array(nums.length) 4 const output = new Array(nums.length) 5 6 /* Calculate prefix products */ 7 let prefixProduct = 1 8 for (let i = 0; i < nums.length; i++) { 9 prefixProduct = prefixProduct * nums[i] 10 prefixArr[i] = prefixProduct 11 } 12 13 /* Calculate suffix products */ 14 let suffixProduct = 1 15 for (let i = nums.length - 1; i >= 0; i--) { 16 suffixProduct = suffixProduct * nums[i] 17 /* Note that we are adding from the end here */ 18 suffixArr[i] = suffixProduct 19 } 20 21 for (let i = 0; i < nums.length; i++) { 22 if (i === 0) { 23 output[i] = suffixArr[i + 1] 24 } else if (i === nums.length - 1) { 25 output[i] = prefixArr[i - 1] 26 } else { 27 output[i] = prefixArr[i - 1] * suffixArr[i + 1] 28 } 29 } 30 31 return output 32}; 33
Time Complexity: O(n)
Space Complexity: O(n)
Optimized Approach 3
This is a variation of the Optimal Approach 2 where instead of using two separate arrays for holding the prefix and suffix products, we use the output array to first store the prefix products and then update it using suffix products to get the desired output. This reduces the space complexity from O(n) to O(1).
- Calculate the prefix products and save it to the output array
- Loop through the
numsarray from the end, calculate the suffix product at each element and use the same formula as before to get the desired output -prefix[i-1] * suffix[i+1]. Since the output array has the prefix products, the formula can be represented asoutput[i-1] * suffix[i+1].- When
i = 0, sinceoutput[i-1]will not be available, the desired output issuffix[i+1] - When
i = n-1, sincesuffix[i+1]will not be available, the desired output isoutput[i-1] - For all other indexes, the desired output is
output[i-1] * suffix[i+1]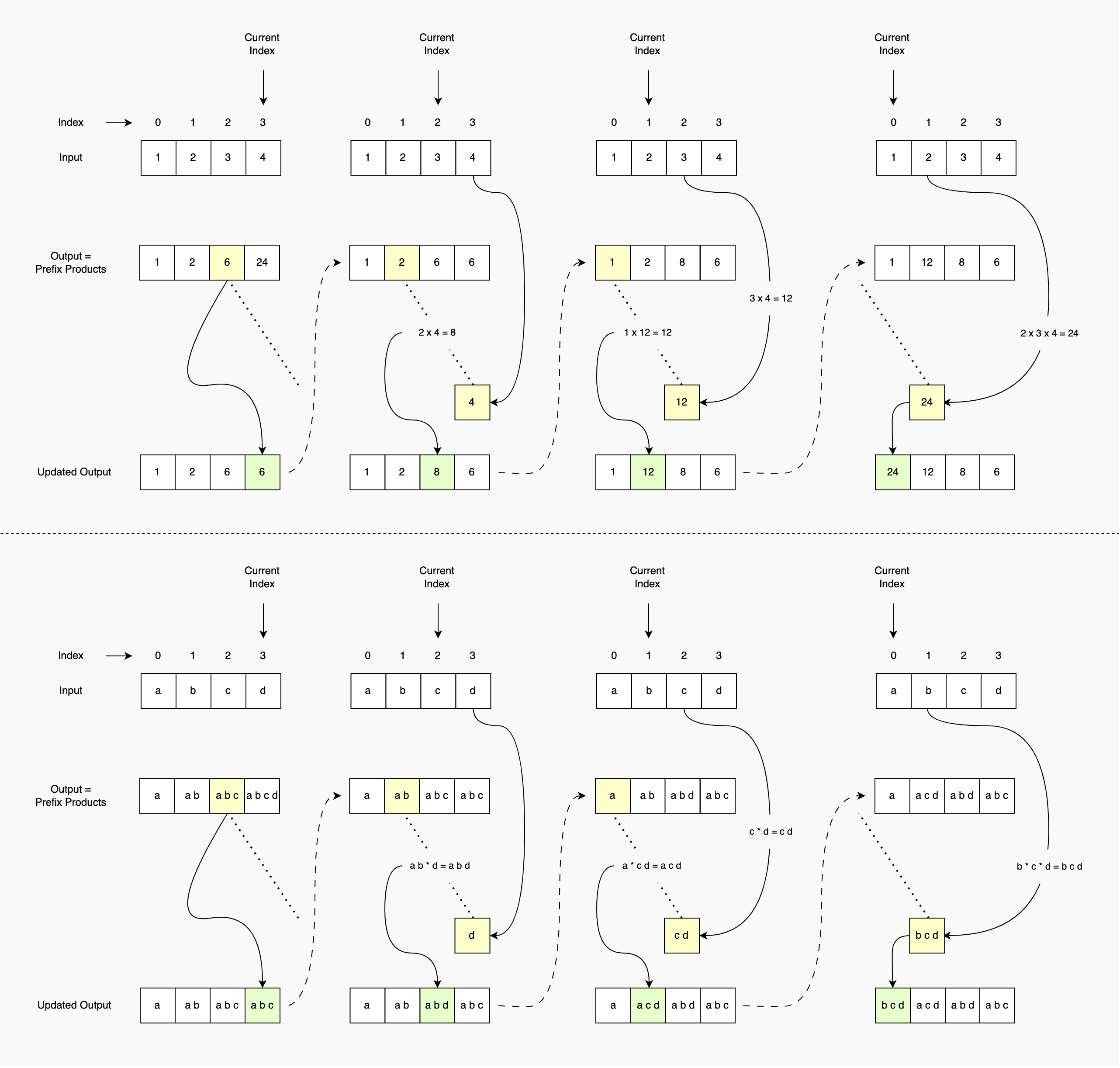
- When
1var productExceptSelf = function (nums) { 2 const output = new Array(nums.length) 3 4 /* Calculate prefix products and save to output */ 5 let prefixProduct = 1 6 for (let i = 0; i < nums.length; i++) { 7 prefixProduct = prefixProduct * nums[i] 8 output[i] = prefixProduct 9 } 10 11 /* Calculate suffix products and update output array */ 12 let suffixProduct = 1 13 for (let i = nums.length - 1; i >= 0; i--) { 14 // Don't calculate the suffixProduct here since we need the 15 // suffix product to not include the current element 16 if (i === 0) { 17 output[i] = suffixProduct 18 } else if (i === nums.length - 1) { 19 output[i] = output[i - 1] 20 } else { 21 output[i] = output[i - 1] * suffixProduct 22 } 23 // Instead, do it here, 24 // so that the next iteration gets the current element product 25 suffixProduct = suffixProduct * nums[i] 26 } 27 28 return output 29}; 30
Time Complexity: O(n)
Space Complexity: O(1)
I hope this was helpful!